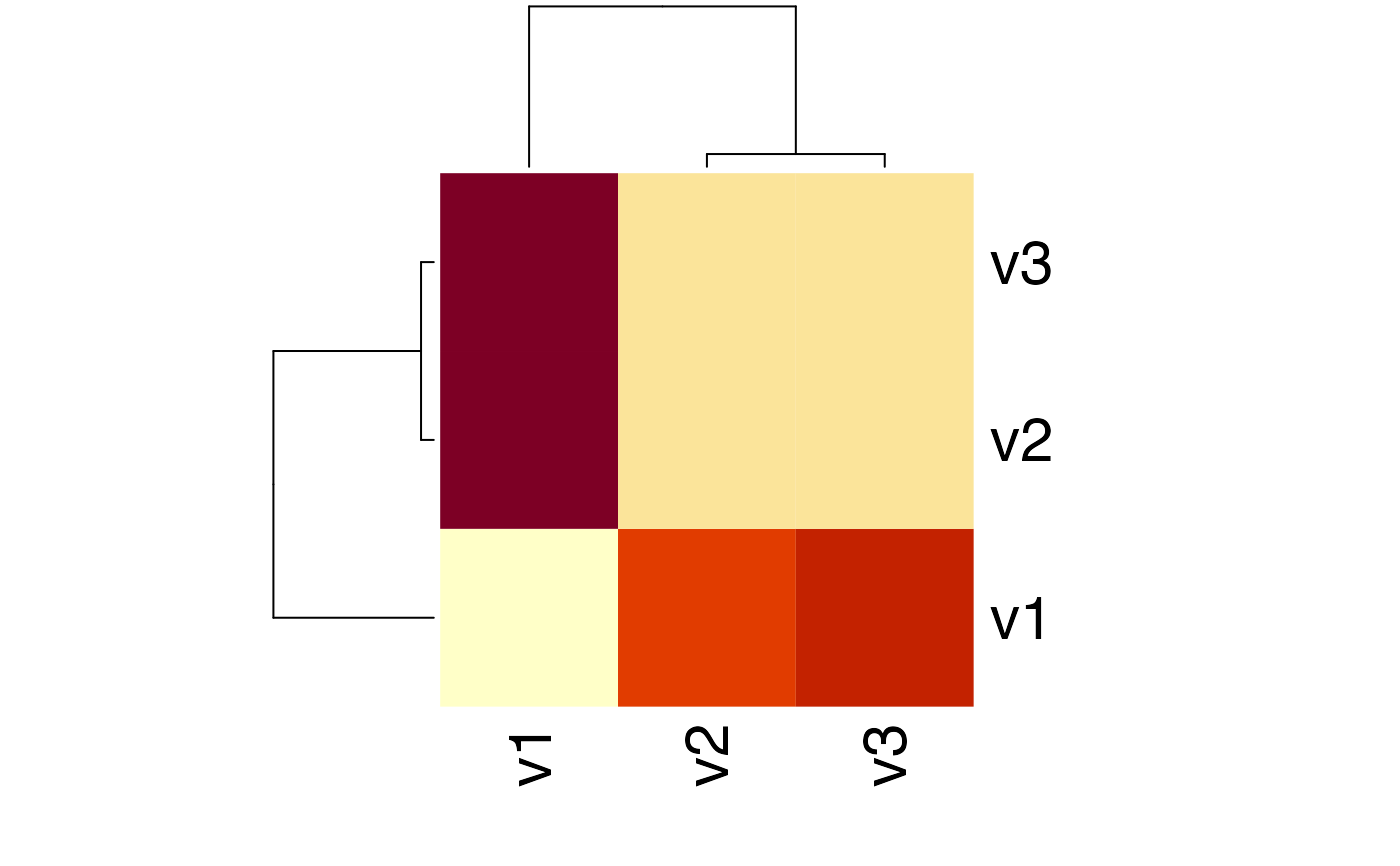Kullback-Leibler Divergence

This function computes the Kullback-Leibler divergence of two probability distributions P and Q.

KL(x, test.na = TRUE, unit = "log2", est.prob = NULL, epsilon = 1e-05)

Arguments

x: a numeric data.frame or matrix (storing probability vectors) or a numeric data.frame or matrix storing counts (if est.prob = TRUE). See distance for details.
test.na: a boolean value indicating whether input vectors should be tested for NA values.
unit: a character string specifying the logarithm unit that shall be used to compute distances that depend on log computations.
est.prob: method to estimate probabilities from a count vector. Default: est.prob = NULL.
epsilon: a small value to address cases in the KL computation where division by zero occurs. In these cases, x / 0 or 0 / 0 will be replaced by epsilon. The default is epsilon = 0.00001. However, we recommend to choose a custom epsilon value depending on the size of the input vectors, the expected similarity between compared probability density functions and whether or not many 0 values are present within the compared vectors. As a rough rule of thumb we suggest that when dealing with very large input vectors which are very similar and contain many 0 values, the epsilon value should be set even smaller (e.g. epsilon = 0.000000001), whereas when vector sizes are small or distributions very divergent then higher epsilon values may also be appropriate (e.g. epsilon = 0.01). Addressing this epsilon issue is important to avoid cases where distance metrics return negative values which are not defined and only occur due to the technical issues of computing x / 0 or 0 / 0 cases.

Value

The Kullback-Leibler divergence of probability vectors.

Details

$$KL(P||Q) = \sum P(P) * log2(P(P) / P(Q)) = H(P,Q) - H(P)$$

where H(P,Q) denotes the joint entropy of the probability distributions P and Q and H(P) denotes the entropy of probability distribution P. In case P = Q then KL(P,Q) = 0 and in case P != Q then KL(P,Q) > 0.

The KL divergence is a non-symmetric measure of the directed divergence between two probability distributions P and Q. It only fulfills the positivity property of a distance metric.

Because of the relation KL(P||Q) = H(P,Q) - H(P), the Kullback-Leibler divergence of two probability distributions P and Q is also named Cross Entropy of two probability distributions P and Q.

References

Cover Thomas M. and Thomas Joy A. 2006. Elements of Information Theory. John Wiley & Sons.

Author

Hajk-Georg Drost

Examples


# Kulback-Leibler Divergence between P and Q
P <- 1:10/sum(1:10)
Q <- 20:29/sum(20:29)
x <- rbind(P,Q)
KL(x)
#> Metric: 'kullback-leibler' using unit: 'log2'; comparing: 2 vectors.
#> kullback-leibler 
#>        0.1392629 

# Kulback-Leibler Divergence between P and Q using different log bases
KL(x, unit = "log2") # Default
#> Metric: 'kullback-leibler' using unit: 'log2'; comparing: 2 vectors.
#> kullback-leibler 
#>        0.1392629 
KL(x, unit = "log")
#> Metric: 'kullback-leibler' using unit: 'log'; comparing: 2 vectors.
#> kullback-leibler 
#>       0.09652967 
KL(x, unit = "log10")
#> Metric: 'kullback-leibler' using unit: 'log10'; comparing: 2 vectors.
#> kullback-leibler 
#>        0.0419223 

# Kulback-Leibler Divergence between count vectors P.count and Q.count
P.count <- 1:10
Q.count <- 20:29
x.count <- rbind(P.count,Q.count)
KL(x, est.prob = "empirical")
#> Metric: 'kullback-leibler' using unit: 'log2'; comparing: 2 vectors.
#> kullback-leibler 
#>        0.1392629 

# Example: Distance Matrix using KL-Distance

Prob <- rbind(1:10/sum(1:10), 20:29/sum(20:29), 30:39/sum(30:39))

# compute the KL matrix of a given probability matrix
KLMatrix <- KL(Prob)
#> Metric: 'kullback-leibler' using unit: 'log2'; comparing: 3 vectors.

# plot a heatmap of the corresponding KL matrix
heatmap(KLMatrix)